
Zadanie Termity [A] (ter)
Pomóż nam usprawnić bazę zadań!
Termity [A]
Limit pamięci: 256 MB
Dwa termity postanowiły zjeść stary, drewniany płot. Płot ów składa się z  sztachet, których wysokości niekoniecznie są jednakowe.
Termity pożarły już część z nich, ale stwierdziły, że warto tę pracę urozmaicić.
Zdecydowały zagrać w grę i jeść na przemian po jednej sztachecie.
Termit w przypadającej na niego kolejce może wybrać do zjedzenia tylko taką sztachetę,
która sąsiaduje z jakąś wcześniej pożartą sztachetą.
Wiedząc, że każdy z termitów tak wybiera sztachety, by w ciągu całej gry suma wysokości
zjedzonych przez niego sztachet była jak największa, oblicz, ile drewna przypadnie każdemu z nich w udziale.
sztachet, których wysokości niekoniecznie są jednakowe.
Termity pożarły już część z nich, ale stwierdziły, że warto tę pracę urozmaicić.
Zdecydowały zagrać w grę i jeść na przemian po jednej sztachecie.
Termit w przypadającej na niego kolejce może wybrać do zjedzenia tylko taką sztachetę,
która sąsiaduje z jakąś wcześniej pożartą sztachetą.
Wiedząc, że każdy z termitów tak wybiera sztachety, by w ciągu całej gry suma wysokości
zjedzonych przez niego sztachet była jak największa, oblicz, ile drewna przypadnie każdemu z nich w udziale.
Wejście
W pierwszym wierszu standardowego wejścia znajduje się liczba całkowita  (
(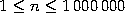 ), określająca liczbę sztachet w płocie.
Drugi wiersz zawiera ciąg
), określająca liczbę sztachet w płocie.
Drugi wiersz zawiera ciąg  liczb całkowitych
liczb całkowitych 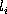 (
(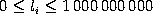 ), opisujących wysokości kolejnych sztachet, przy czym
), opisujących wysokości kolejnych sztachet, przy czym 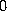 oznacza zjedzoną sztachetę.
Sztacheta o numerze
oznacza zjedzoną sztachetę.
Sztacheta o numerze  (dla
(dla 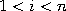 ) sąsiaduje ze sztachetami o numerach
) sąsiaduje ze sztachetami o numerach 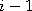 oraz
oraz 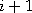 ,
sztacheta o numerze
,
sztacheta o numerze 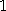 sąsiaduje tylko ze sztachetą o numerze
sąsiaduje tylko ze sztachetą o numerze 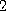 , a sztacheta o numerze
, a sztacheta o numerze  tylko ze sztachetą o numerze
tylko ze sztachetą o numerze 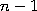 .
Co najmniej jedna z liczb
.
Co najmniej jedna z liczb 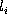 na wejściu będzie równa zeru.
na wejściu będzie równa zeru.
Wyjście
W pierwszym i jedynym wierszu standardowego wyjścia należy wypisać dwie liczby całkowite. Pierwsza z nich określa sumę wysokości sztachet, którymi pożywi się termit rozpoczynający rozgrywkę, zaś druga, ile drewna przypadnie jego przeciwnikowi.
Przykład
Dla danych wejściowych:
8 1 2 0 3 7 4 0 9
poprawną odpowiedzią jest:
17 9
Wyjaśnienie do przykładu: Płot składał się z 8 sztachet, z których 2 już są zjedzone. Pierwszy termit w pierwszym ruchu może wybrać sztachety o wysokościach 2, 3, 4 lub 9. W trakcie optymalnej rozgrywki jedzone będą kolejno sztachety o wysokościach 9, 2, 1, 4, 7 i 3.
Autor zadania: Tomasz Idziaszek.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English